匈牙利算法学习

秦篆原创大约 6 分钟

最近忙完了省石化的紧急需求，终于得空刷刷题目了，今天遇到的题是化为机试的HJ28，从而了解到匈牙利算法。这玩意可比之前的动态规划简单多了，下面一起来看看吧~~

匈牙利算法用来解决什么问题？

一般用于解决图论中的二分图求解最大匹配数和最小覆盖数的问题下面是一个常见的二分图样例：

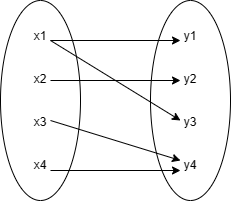
图中的实线表示集合x中的x？元素能与集合y中的元素y？形成一条有效边。

网络上有很多匈牙利算法的解法，我也是从前辈们的思想中学习的，那我这里就以HJ28这道题为切入点，讲讲通过匈牙利算法求得最大匹配数的问题。

HJ28

描述
若两个正整数的和为素数，则这两个正整数称之为“素数伴侣”，如2和5、6和13，它们能应用于通信加密。现在密码学会请你设计一个程序，从已有的 N （ N 为偶数）个正整数中挑选出若干对组成“素数伴侣”，挑选方案多种多样，例如有4个正整数：2，5，6，13，如果将5和6分为一组中只能得到一组“素数伴侣”，而将2和5、6和13编组将得到两组“素数伴侣”，能组成“素数伴侣”最多的方案称为“最佳方案”，当然密码学会希望你寻找出“最佳方案”。

输入:
有一个正偶数 n ，表示待挑选的自然数的个数。后面给出 n 个具体的数字。输出: 输出一个整数 K ，表示你求得的“最佳方案”组成“素数伴侣”的对数。

输入描述：
输入说明
1 输入一个正偶数 n
2 输入 n 个整数

输出描述：
求得的“最佳方案”组成“素数伴侣”的对数。

分析

素数由于只能由自己和1整除的特性，必然是一个偶数与一个奇数的和形成的某数，所以我们将传入的字符串先分割为奇数串和偶数串

let N = 0 //左侧数组长度
let M = 0 //右侧数组长度
let k = 0 //记录输入字符串长度，同时用于判断是否第一次输入
let odds:number[] = [] //奇数串
let evens:number[] = [] //偶数串
let eToO:any = [] //记录当前偶数匹配的奇数定位
let oddStatus:any = [] //记录当前奇数是否被访问过
let mapPrime:any = [] // 左侧和右侧的公共边（两数相加能为素数）
rl.on("line",(line:string) => {
    if (k === 0) k = Number(line)
    else {
        let temp = line.split(" ").map(Number)
        for (let number of temp) {
            if (even(number)){
                evens.push(number)
            }else {
                odds.push(number)
            }
        }
    }
})

然后需要计算偶数集合和奇数集合元素相加为素数的元素是哪些，也就是形成了有效边。

N = evens.length
M = odds.length
eToO = new Array(M).fill(-1) //初始化长度为奇数（右侧）长度的数组，初始匹配位置不能大于0
mapPrime = new Array(N).fill(undefined).map(()=>{
    return  new Array(M).fill(false)
}) //初始化公共边数量为0
// 初始化map,eToO,oddStatus
for (let i = 0; i < N; i++) {
    for (let j = 0; j < M; j++) {
        if (prime(evens[i]+odds[j])){
            mapPrime[i][j] = true
        }
    }
}

初始化mapPrime之后，就进入了匈牙利算法的主题，这里我们就以集合 3,7,9,2,6,14为例

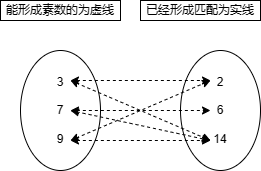
从图中可以直观的看到，3能与2和14组成素数，7能与6和14组成素数，而9分别能与2和14组成素数。按照匈牙利算法，先到先得，能让就让的思想，我们开始分析这个图。从左边的奇数开始。
我们先找到奇数3，发现他一开始就能能与偶数2组成素数，由于2还没有被绑定过关系，所以先给3和2做一个绑定关系，请注意我们现在做的所有操作都是在设想阶段，并没有实际的给数字做了唯一的绑定关系，后面如果有其它数组能够匹配的话，这个关系是能够被替换掉的。所以上面的图变成了这样。

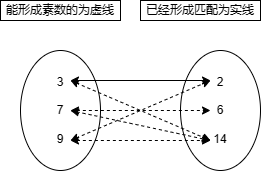
接下来我们继续看7，发现它能与偶数6和14形成素数，由于6还没有被绑定过关系，所以给7与6形成绑定关系

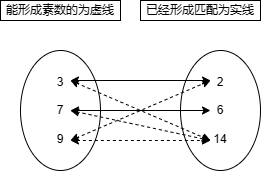
然后看最后一个9，它既能与2形成素数也能与14形成素数，所以先判断2有没有被匹配过，因为2被3匹配过了。按照匈牙利算法的能让就让的思想，这里我们需要解判断3能不能找到新的对应匹配，发现3也能和14进行绑定，可以将2让出来给9，所以3最后与14进行绑定，得到下面的状态。

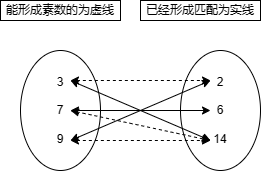
所以最后所有人都得到了响应匹配的位置，所以得到最大匹配数为3。

结论

最后的代码如下

//HJ28
const prime = (num:any): boolean => {
    debugger
    if (num < 2) {
        return false;
    }
    for (let i = 2; i < num; i++) {
        if (num % i == 0) {
            return false;
        }
    }
    return true;
}
const even  = (num:number|any):boolean => {
    return num%2 === 0
}

let N = 0 //左侧数组长度
let M = 0 //右侧数组长度
let k = 0 //记录输入字符串长度，同时用于判断是否第一次输入
let odds:number[] = [] //奇数串
let evens:number[] = [] //偶数串
let eToO:any = [] //记录当前偶数匹配的奇数定位
let oddStatus:any = [] //记录当前奇数是否被访问过
let mapPrime:any = [] // 左侧和右侧的公共边（两数相加能为素数）
rl.on("line",(line:string) => {
    if (k === 0) k = Number(line)
    else {
        let temp = line.split(" ").map(Number)
        for (let number of temp) {
            if (even(number)){
                evens.push(number)
            }else {
                odds.push(number)
            }
        }
        N = evens.length
        M = odds.length
        eToO = new Array(M).fill(-1) //初始化长度为奇数（右侧）长度的数组，匹配位置不能大于0
        mapPrime = new Array(N).fill(undefined).map(()=>{
            return  new Array(M).fill(false)
        }) //初始化公共边数量为0
        // 初始化map,eToO,oddStatus
        for (let i = 0; i < N; i++) {
            for (let j = 0; j < M; j++) {
                if (prime(evens[i]+odds[j])){
                    mapPrime[i][j] = true
                }
            }
        }
        let res = 0
        for (let i = 0; i < N; i++) { //开始遍历偶数列表
            oddStatus = new Array(M).fill(false) //初始化访问状态为false 全未访问
            if (HJ28(i)){
                res++
            }
        }
        console.log(res)
        rl.close()
    }
})



//HJ28
const HJ28 = (i:number):boolean => {
    for (let j = 0; j < M; j++) {
        if (mapPrime[i][j] && !oddStatus[j]){ //当前访问的奇数和偶数能组成素数并且当前的奇数没有被访问过
            oddStatus[j] = true //j位置的素数已经访问过了
            if (eToO[j] === -1 || HJ28(eToO[j])){ //当前奇数还没有被匹配过或者当前奇数的原配能够找到另一个
                eToO[j] = i
                return true
            }
        }
    }
    return  false
}

匈牙利算法学习

# 匈牙利算法用来解决什么问题？

# HJ28

# 分析

# 结论

匈牙利算法用来解决什么问题？

HJ28

分析

结论